Download this week’s example code here.

So far, we’ve analyzed text (with word counts and n-grams) and we’ve generated texts (with Markov chains and context-free grammars). This week’s material concerns the last puck in the text processing hat-trick: text classification. We’re setting off to answer the following question: how can we programmatically determine if two texts are similar, and to what extent?

Identity: Compare.java

The Compare class implements what is probably the simplest kind of text classification: it checks to see if the texts contained in two files are identical. Here’s the source code:

import com.decontextualize.a2z.TextFilter;
public class Compare {
  public static void main(String[] args) {
    String filename1 = args[0]; // get filenames from command line
    String filename2 = args[1];
    TextFilter tf1 = new TextFilter(); // create new textfilter objects
    TextFilter tf2 = new TextFilter();
    String text1 = tf1.collectString(TextFilter.fromFile(filename1));
    String text2 = tf2.collectString(TextFilter.fromFile(filename2));
    if (text1.equals(text2)) {
      System.out.println("identical");
    }
    else {
      System.out.println("different");
    }
  }
}

Run the program, giving it two arguments on the command line. The program will print identical if the two files contain exactly the same text, and different otherwise. Example:

$ java Compare file1.txt file2.txt
identical

This program is somewhat unusual, as we’re not extending TextFilter. This program doesn’t read from the UNIX standard input; you can’t (e.g.) use < to send input to it. Instead, it reads from two files, which you specify on the command line when you run the program.

Args

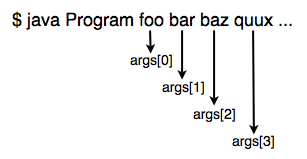
Aside from standard input, the main way to give information to a program that you run from the UNIX command line is through arguments—little bits of text that come after the file name. We saw these in action back in week 1: when we ran grep foo, we were sending the string foo to the grep command as an argument.

Java programs can take arguments from the command line as well. Here’s how it works: whenever you run a Java program from the command line, everything after java YourProgram is passed as an array of strings to the main method of your class—that’s the String[] args that’s a part of the declaration of the main method. Command line arguments use white space as a delimiter, so running (e.g.) java YourProgram george nancy jimbo would result in the args array having george in index 0, nancy in index 1, and jimbo in index 2. Here’s a diagram of how command line arguments get assigned to indices of args:

How command-line arguments get assigned to args

You can specify as many (or as few) command-line arguments as you’d like. You can even check the length of the arguments array (args.length) to see how many arguments were passed to your program, and adjust the behavior of your program accordingly.

(Note: redirected files—i.e., <some_file.txt—and piped commands don’t show up in args. Those are for UNIX to interpret: Java doesn’t know that they were ever there.)

TextFilter vanilla

So now we can get arguments from the command line. In Compare, we’re using the first two arguments on the command line to specify filenames: namely, the two files we want to compare. What we’d really like to do is grab the entire contents of both files into two big strings, so we can compare them to one another.

Java (for better or worse) has no direct analogue to PHP’s file_get_contents function or Python’s file.read(), so if we want to get an entire file (rather than process it line by line or character by character), we have to improvise. The TextFilter class has two properties that will help us out with this task.

First off, the TextFilter class defines a useful default behavior, even if you don’t extend it. Most of the programs we’ve written so far that extend TextFilter redefine the eachLine method. The default behavior for eachLine—what happens if you use TextFilter without writing a class that extends it—is simply to print out each line as it comes in. The source code looks like this:

  protected void eachLine(String line) {
    println(line);
  }

So, if we create an instance of TextFilter and call collectString on it, we should get back a string containing the contents of UNIX standard input. (The collectString and collectLines methods were discussed in week 4.) We don’t want to read from standard input, however, so we have to pass in an argument that tells TextFilter to look for its input from a file. The method TextFilter.fromFile does just that. (For the interested, fromFile returns a java Reader object—which, coincidentally, is the same thing that Processing’s createReader function returns.)

Putting it all together:

TextFilter tf1 = new TextFilter();
String text1 = tf1.collectString(TextFilter.fromFile(filename1));

Line 1 creates a new TextFilter object. Line 2 tells that TextFilter object the following: “Hey, there’s a file name in a string called filename1. Read every line from that file, collect all of those lines into a string, and give it back to me.”

Not all equals are created equal

There’s one last tricky part in Compare: actually comparing the strings. It turns out that the comparison operator == that you know and love doesn’t work for strings—in fact, it doesn’t work for anything other than primitives. (We discussed the difference between primitives and objects in Java in Week 4.) (Here’s a good explanation of what’s happening behind the scenes.)

In order to check to see if two strings are equal, you need to use the equals method of the string object, which takes another string as a parameter. It’ll return true if the strings are equal, and false otherwise. Here’s the bit of code that compares strings from Compare.java:

    if (text1.equals(text2)) {
      System.out.println("identical");
    }
    else {
      System.out.println("different");
    }

Keyword-based classification

Perhaps the next-to-simplest kind of text classification is keyword-based classification, in which we classify texts based on the presence of certain keywords in that text. Let’s say that we want to determine whether some arbitrary text was written by Mark Twain. We might write up the following list of keywords:

Mississippi
river
Sawyer
whitewash
treasure
gold
widow
raft
widow
steamboat
yankee

… and stipulate that the higher the frequency of these words in a particular text, the more likely it is that the text was written by Mark Twain. (This stipulation probably doesn’t reflect reality, as we’ll see, but stick with me for a bit.)

KeywordClassifier.java is a simple program for performing keyword-based classification. It works like this:

$ java KeywordClassifier keyword_list.txt <text_to_score.txt

… where keyword_list.txt is a file that contains a list of keywords, one keyword per line (see twainwords.txt in this week’s examples), and the text to be classified is passed in on standard input. You’ll get back the number of “hits”—the number of times any keyword was found in the input—and a “score,” whose exact method of calculation we’ll see below. The main gist is that the higher the score, the more likely a text is to belong to the category specified by the keyword list. Here’s a transcript of an example session (using the text files in this week’s example code):

$ java KeywordClassifier twainwords.txt <twain.txt
Hits: 420
Score: 1.3366984185584663
$ java KeywordClassifier twainwords.txt <roughing_it.txt 
Hits: 128
Score: 0.7100381645513446
$ java KeywordClassifier twainwords.txt <austen.txt 
Hits: 26
Score: 0.06289095192712389

As you can see, the score for twain.txt (which contains selected works of Twain) and roughing_it.txt (which contains Twain’s non-fiction work Roughing It) score much higher than austen.txt (which contains selected works of Jane Austen). So far so good!

KeywordClassifier.java

Here’s the source code for our keyword classification program in full:

import com.decontextualize.a2z.TextFilter;
public class KeywordClassifier extends TextFilter {
  public static void main(String[] args) {
    String filename = args[0];
    String[] contents = new TextFilter().collectLines(fromFile(filename));
    KeywordClassifier kwc = new KeywordClassifier();
    kwc.setKeywords(contents);
    kwc.run();
  }
  private String[] keywords;
  private int hits;
  private int tokenTotal;
  public void setKeywords(String[] keywords_) {
    keywords = keywords_;
  }
  public void eachLine(String line) {
    String[] tokens = line.split(" ");
    tokenTotal += tokens.length;
    for (String keyword: keywords) {
      keyword = keyword.toLowerCase();
      for (String token: tokens) {
        token = token.toLowerCase();
        if (token.equals(keyword)) {
          hits++;
        }
      }
    }
  }
  public void end() {
    double score = hits / (double)tokenTotal * 1000;
    println("Hits: " + String.valueOf(hits));
    println("Score: " + String.valueOf(score));
  }
}

In the main method, we create a TextFilter that collects all of the lines from the file given on the command line into an array of strings, which it then passes to the setKeywords method of the KeywordClassifier object. In eachLine, we first break up the line into words using split; then we increase the tokenTotal variable by the number of words in line. (The tokenTotal variable will eventually contain the total number of words in the file.)

The bulk of the work happens in the nested for loops there in eachLine. The outer loop iterates over every keyword; the inner loop iterates every word in the line. If the word from the line and the keyword match, we have a hit, and the hits variable gets incremented by one. By the time we reach the end of the file, every word in the source text will have been compared to every word in the keyword list.

In end, we give a score to the text. This score is percentage of words in the source text that matched any keyword, multiplied by 1000 to make the number easier to read. If a text consisted of nothing but keywords, its score would be 1000; if it contained no keywords at all, its score would be 0.

Keyword drawbacks

At first blush, we get good results from our keyword classifier. Texts we know to have been written by Twain get high scores; texts we know to have been written by other authors get lower scores. But what if we fed our classifier the following text, written by yours truly:

“Two Keyword-Matching Twain Haiku”

oh the mighty
Mississippi river — gold
steamboats and widows

No yankee whitewash
Mississippi steamboats and
river rafts floating

–Adam Parrish

This brief compendium of canon-worthy poetic genius is included in this week’s examples as fake_twain.txt. Let’s pass it to KeywordClassifier and see what happens:

$ java KeywordClassifier twainwords.txt <fake_twain.txt
Hits: 7
Score: 200.0

Whoops! A staggering score of 200—far higher than either of the texts we know to have been written by Twain!

This demonstrates one of the flaws of keyword-based classification algorithms: they’re prone to false identification. It’s easy, for example, to game the system either by constructing a text that matches the keywords exactly (as fake_twain.txt does), or skirts around the keywords to avoid identification (which is why you get so many e-mails with “v1agr@” in the subject line).

Another disadvantage of keyword-based systems is that you have to come up with the list of keywords on your own—or you have to write a program to do it for you. Your first idea might be to make a program that finds the most common words in a text, and use those as keywords. The problem with that, of course, is that the most frequent words in English—e.g., the, and, a, to, of, I—are equally common across all texts.

No, what we need is an algorithm that determines not just how frequently a given token occurs in a text, but how frequently it occurs in a text compared to how frequently it occurs in another text. A Bayesian classifier does exactly that. The next section will take you through the logic behind Bayesian text classification, and a simple Java implementation of the algorithm.

Bayesian text classification

(The code in this section owes much of its existence to John Graham-Cumming’s Perl implementation of Bayesian classification from Dr. Dobb’s Journal.)

I’m not going to address the high falutin’ math of Bayes’ Theorem here, as others have done it better elsewhere—and, it turns out, you don’t have to understand all of the theorem’s intricacies to be able to apply it to text classification. Bayes’ Theorem is more or less a mathematical restating of the phrase “correlation is not causation,” and that’s the idea that we’re trying to apply here to text classification.

More specifically, our Bayesian classification program relies on the following data: the extent to which a given token isn’t just frequent in a given text, but uniquely frequent in that text. Taking a spam filter as an example: the word “the” probably occurs just as much in spam as it does in e-mail that I want to keep, so finding the word “the” in an e-mail isn’t a good indicator of a message’s spamminess. The word “viagra,” on the other hand, frequently occurs in spam, but (as I am a thoroughly virile man) almost never occurs in legitimate e-mail; if it’s found in an e-mail message, that’s a good indicator that the message is spam. The word “python” works the other way: I get lots of legitimate e-mail with that term, but hardly any spam. To quote Paul Graham, “a word like that is effectively a kind of password for sending mail to me.”

Twain v. Shakespeare: FIGHT

Let’s say that we’re building a new text classifier: it’s going to tell us whether or not a given text is more likely to have been written by Shakespeare or Mark Twain. We’re going to need two texts to “train” our program; we’ll call these the category texts. The training procedure consists of gathering the following data: for each token—in either category text—determine how much of that text is made up of that token. After we’ve completed the training process, we’ll have a data structure in memory (a HashMap, to be precise) that maps every token to that token’s percentage.

For example: if our Twain category text contains 1000 words total, and the word “of” occurs 50 times, then “of” makes up 5% (50/1000) of that text. Likewise, if our Shakespearean category text contains 5000 words total, and the word “of” occurs 200 times, then “of” makes up 4% (200/5000) of that text. The word “king” might comprise 0.04% of all tokens in the Shakespeare category text, but 0.0087% of all tokens in the Twain category text; and so forth.

When we’re done training, we pass the algorithm a text to classify. Let’s say that we want to see whether “the cat in the hat” is more likely to have been written by Shakespeare or Twain. We’ll call “the cat in our hat” our input text. (Not the book The Cat in the Hat—the literal string “the cat in the hat.”) We’re going to give the text two scores: one for Shakespeare and one for Twain. That scores are calculated like this (warning: handwaving ahead):

Shakespeare score =
    (Shakespeare% "the")
  x (Shakespeare% "cat")
  x (Shakespeare% "in")
  x (Shakespeare% "hat")
  x (total tokens in Shakespeare / total tokens in all category texts)

Twain score =
    (Twain% "the")
  x (Twain% "cat")
  x (Twain% "in") 
  x (Twain% "hat")
  x (total tokens in Twain / total tokens in all category texts)

Read “Shakespeare%” above as “the percentage of the Shakespeare category text comprised by the following token”; likewise for “Twain%.” Again, no detailed explanations of the why this formula works—but what we’re essentially doing is calculating the combined probability that a given sequence of tokens will occur in either of our category texts. (The final multiplier in the score calculations above compensates for the fact that our category texts might have different numbers of words in them; the scores must be weighted accordingly.)

After performing these calculations, we’ll end up with two numbers: one score for Shakespeare, and one for Twain. The highest score between those two tells us to which category our input text belongs.

Our implementation

Our Java implementation of the above formula consists of two classes. The first, BayesCategory, keeps track of a single category text: it keeps track of all unique tokens in a category text, how frequently those tokens occur, and has the ability to score an input text according to that category. The second class, BayesClassifier, keeps track of the input text, and manages BayesCategory objects. We’ll talk about BayesCategory first.

BayesCategory.java

The BayesCategory class keeps track of what words occur in a category text, and how frequently those words occur. It’s a lot like the Concordance class from week 4, except it does two things a regular concordance doesn’t do. First, it can return the percentage for a given word: the number of times a word occurs in the category text, divided by the total number of terms in the text; second, it can perform the calculation above, evaluating for an incoming text how similar that text is to the category text.

But before we look at the BayesCategory methods percentage and score, let’s take a look at train.

  public void train(String word) {
    if (count.containsKey(word)) {
      count.put(word, count.get(word) + 1);
    }
    else {
      count.put(word, 1);
    }
    total++;
  }

The count variable is a HashMap that maps string to integers; total is an integer. This code should look familiar: it’s almost exactly the same code that we’d use to add a word to the WordCount object (again, from week 4). For every word that comes in, we either add it to our HashMap or increment the count for that word in the HashMap. We also increment total—once we’ve finished parsing the category text, this variable will contain the total number of words in the text.

The source code for percentage:

  public double percentage(String word) {
    if (count.containsKey(word)) {
      return count.get(word) / (double)total;
    }
    else {
      return 0.01 / (double)total;
    }
  }

This method takes a word as an argument, and returns the number of times the given word occurs in the category text divided by the total number of words in the category text. This is where we’re going to get the “Shakespeare%” and “Twain%” number that we used in the formula above. If the word passed in to the method wasn’t found in the category text (i.e., if it’s not in the HashMap), then we return a very small number.

Why not just return zero if the word wasn’t found? For one thing, that would mess up our formula: any number multiplied by zero is zero, so if *any* word was found in the input text that isn’t in the category text, the input text would automatically get a score of zero. (Re-check the formula above to verify that I’m right.) We’re going to give the input text the benefit of the doubt: we’re saying, “it’s okay, input text! I’m not going to count this unknown word against you. We’ll just say that the word might have occurred in the category text, but with a very small probability.”

Score!

Now that we have all of our category words stored, and we have the ability to get percentages for each of those words, we can talk about the scoring algorithm. Here’s the source code of the score method:

  public double score(HashSet<String> src, int totalAll) {
    double scoreVal = 0;
    for (String word: src) {
      double percent = percentage(word);
      scoreVal += Math.log(percent);
    }
    scoreVal += Math.log(total / (double)totalAll);
    return scoreVal;
  }

The method takes two arguments: a HashSet of strings, which contains the unique words of the input text (i.e., the text that we want to classify). The second argument is the total number of words in all categories—not just for this category text, but all other category texts that we want to score the input text against. (We’ll see how this works when we talk about the BayesClassifier class).

The score is initially zero. We loop through every word in the input text (src), calculating the percentage of that word; we then add the logarithm of that value to the score. Then we add the logarithm of the total number of words in this category divided by the total number of words in all categories.

“Hold up,” I hear you saying. “Hold up just a second. Logarithm?! I thought you said no math! And what does this have to do with calculating the score?” Okay, yeah, I sprung that one on you—but for a good reason. Take a look at our formula for calculating the score for a text again. You’ll notice that we’re going to end up multiplying a bunch of very small numbers together:

score =
    percentage("the") -> 0.05
  x percentage("cat") -> 0.0001
  x percentage("in") -> 0.004
  x percentage("hat") -> 0.00004
  ...

(Those numbers are made up, but probably aren’t too far off the mark.) Even after just four words, we have a very, very small number: 0.00000000000008! A number that small is not just difficult to read; it’s bordering on the computer’s precision limit for floating-point numbers. To circumvent both of these problems, we’re going to add together the logarithms of each score. This works because of the following relationship:

   log(a * b * c * ...) = log(a) + log(b) + log(c)

In other words, taking the logarithm of all of the values multiplied together is the same as adding together the logarithm of each value. The advantage of using the logarithm method is that we get numbers that are easier to read; as a side benefit, the calculation goes faster (it’s easier to add numbers than it is to multiply them).

BayesClassifier.java

The BayesClassifier class is the one we’re actually going to run to do text classification. Here’s how to use it:

$ java BayesClassifier shakespeare.txt twain.txt <roughing_it.txt

… where shakespeare.txt and twain.txt are your category texts, and your input text is passed in as standard input. Here, we’re using Twain’s Roughing It as a sample input text, scoring it against the works of Shakespeare and the works of Twain. The output will look something like this:

shakespeare.txt: -402020.9248488622
twain.txt: -381745.6165720206

A higher score is better. The output of this run of the program indicates that our input text was more like twain.txt than it was like shakespeare.txt—exactly the results we were hoping for!

Let’s take a look at how it works. Here’s the (slightly abbreviated) listing of BayesClassifier.java:

import java.util.ArrayList;
import java.util.HashSet;
import com.decontextualize.a2z.TextFilter;
public class BayesClassifier extends TextFilter {
  private ArrayList<BayesCategory> categories = new ArrayList<BayesCategory>();
  private HashSet<String> uniqueWords = new HashSet<String>();

  public static void main(String[] args) {
    BayesClassifier bc = new BayesClassifier();
    for (int i = 0; i < args.length; i++) {
      bc.addCategory(args[i]);
    }
    bc.run();
  }

  public void addCategory(String fname) {
    BayesCategory cat = new BayesCategory(fname);
    String[] lines = new TextFilter().collectLines(fromFile(fname));
    for (String line: lines) {
      String[] tokens = line.split(" ");
      for (String token: tokens) {
        cat.train(token);
      }
    }
    categories.add(cat);
  }

  public void eachLine(String line) {
    String[] tokens = line.split(" ");
    for (String token: tokens) {
      uniqueWords.add(token);
    }
  }

  public void end() {
    int categoryWordTotal = 0;
    for (BayesCategory bcat: categories) {
      categoryWordTotal += bcat.getTotal();
    }
    for (BayesCategory bcat: categories) {
      double score = bcat.score(uniqueWords, categoryWordTotal);
      println(bcat.getName() + ": " + String.valueOf(score));
    }
  }
}

The object has two data structures: uniqueWords, a HashSet that will contain all unique words in the input text, and categories, an ArrayList of BayesCategory objects. The categories ArrayList is populated in main, which takes every element of the args array and passes it to the addCategory method.

The addCategory method takes a single parameter, and passes that to a new TextFilter object as a filename. The TextFilter object gives us back the entire contents of that file as an array of strings, which we then loop over, passing each token to the train method of a new BayesCategory object. The new BayesCategory object is then added to the categories list.

By the time main has finished looping over args, the categories list will contain one BayesCategory object per filename specified on the command line.

The eachLine method is simple: we’re simply reading each line from input, breaking it up into words, and putting them into a HashSet—just like the UniqueWords class from week 4.

In end, we have to do two things. First, we need to calculate the total number of words in all of the category texts (remember, we need that number to do our Bayesian formula). We accomplish this by looping through the list of categories and calling the BayesCategory object’s getTotal method.

After we’ve done that, we can ask each BayesCategory object in categories to score the input text, passing in our HashSet of unique words from the input text (uniqueWords) and the total number of words in all category texts (categoryWordTotal). Then we print out the score for each category.

The astute reader will note that there’s nothing limiting us to using just two categories; the program will actually accept an arbitrary number of category texts. Let’s say we wanted to see whether sonnets.txt (containing all of Shakespeare’s sonnets) was more likely written by Mark Twain, Jane Austen, or William Shakespeare. We’d run the BayesClassifier program like so: (again, all of these files are available in this week’s example code):

$ java BayesClassifier shakespeare.txt twain.txt austen.txt <sonnets.txt

… and the program would produce the following output:

shakespeare.txt: -59886.12916378722
twain.txt: -64716.741899235174
austen.txt: -66448.68994538345

The highest score goes to shakespeare.txt, which is what we’d expect.

Applications

As you might have guessed by now, we can use this algorithm for purposes other than to tell us who wrote particular texts (especially texts whose authors we already know!). Many spam filters use a Bayesian algorithm very similar to the one we just implemented, except they use “spam” and “not-spam” as their categories (instead of “Shakespeare” and “Twain”). You could try this out for yourself by exporting all of the spam messages from your e-mail program, and some selection of non-spam messages, and use those as category texts while passing an incoming message in as input.

Homework

Due March 24th.

Modify, augment, or replace one of the in-class example programs. Some possibilities:

• Design and implement your own document classification algorithm. (Maybe your algorithm works with only particular kinds of texts; maybe it works with data that isn’t textual at all.) Evaluate your design: how does it work, and how well does it work?
• Rework the Bayesian classification code to work on units other than space-separated tokens. Ideas: make it case-insensitive; split on word boundaries instead of spaces; use some unit other than words (n-grams?). Evaluate your changes: how (if at all) do they improve the program’s ability to reliably classify texts?
• The relevance method of the BayesCategory class tells you how “relevant” a particular word was in placing the source text in a particular category. A relevance close to 1 means that the given word only ever occurred in that category; a relevance close to 0 means that the given word never occurred in that category (but did appear in others). Use this value to create a program that extracts the most meaningful/distinctive words from a text.