Recursion

In programming, recursion is the term for when a function calls itself. For the purposes of this class, recursion is primarily useful as a strategy for dealing with nested data structures. By “nested data structure,” I mean any data structure that contains other data structures within it—especially if those structures themselves contain further nested data structures.

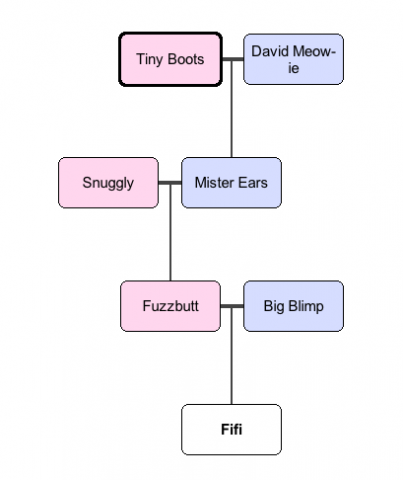
Here’s an easy to understand example: a cat pedigree chart.

Read this chart from bottom to top. Fifi has two parents: Fuzzbutt (the mother, or “queen” in cat fancy terms) and Big Blimp (the “sire”). Each of those cats may, in turn, have parents on the chart. For example: Fuzzbutt’s queen is Snuggly and her sire is Mister Ears; Mister Ears in turn was sired by David Meow-ie, etc.

Given this chart, here’s your task. (1) Figure out how to represent this chart in Python. What kinds of data structures might you use? How might they be related to one another? (2) Write a program that takes this data structure and prints out the names of every cat, regardless of how far up the pedigree they are.

In pursuit of an answer to (1), we might decide to represent a cat as a dictionary, with keys for that cat’s name, sire, and queen:

tree = {
  'name': 'Fifi',
  'queen': {
    'name': 'Fuzzbutt'
  },
  'sire': {
    'name': 'Big Blimp'
  }
}

Simple enough, but we’ve only represented one level of the pedigree. What if we wanted to include Fuzzbutt’s parents as well? We could incorporate those into the same data structure:

tree = {
  'name': 'Fifi',
  'queen': {
    'name': 'Fuzzbutt',
    'queen': {
      'name': 'Snuggly',
    },
    'sire': {
      'name': 'Mister Ears'
    }
  },
  'sire': {
    'name': 'Big Blimp'
  }
}

Now you’re seeing what I meant by “nested data structure.” Each cat is represented by a dictionary, but each of those dictionaries may contain inside it the definition of another cat. If we continue to fill out this structure from the chart, it looks something like this:

tree = {
  'name': 'Fifi',
  'queen': {
    'name': 'Fuzzbutt',
    'queen': {
      'name': 'Snuggly'
    },
    'sire': {
      'name': 'Mister Ears',
      'queen': {
        'name': 'Tiny Boots'
      },
      'sire': {
        'name': 'David Meow-ie'
      }
    }
  },
  'sire': {
    'name': 'Big Blimp'
  }
}

This looks complicated, but it’s actually a one-to-one mapping of the information on the pedigree chart.

(tk)

tree = {
  'name': 'Fifi',
  'queen': {
    'name': 'Fuzzbutt',
    'queen': {
      'name': 'Snuggly'
    },
    'sire': {
      'name': 'Mister Ears',
      'queen': {
        'name': 'Tiny Boots'
      },
      'sire': {
        'name': 'David Meow-ie'
      }
    }
  },
  'sire': {
    'name': 'Big Blimp'
  }
}

def print_cat_names(tree):
  print tree['name']
  if 'queen' in tree:
    print_cat_names(tree['queen'])
  if 'sire' in tree:
    print_cat_names(tree['sire'])

if __name__ == '__main__':
  print_cat_names(tree)

Recursion: the classic example

Here’s a classic example: calculating the sum of a list of numbers. The sum of a list of numbers can be calculated thusly: add the value of the first item of a list to the sum of the remaining items. How to calculate the sum of the remaining items? Well, add the value of the first of the items to the remaining items. And so forth. Here’s a function to do this in Python:

>>> def recursive_sum(n):
...     if len(n) == 1: # "base case"
...             return n[0]
...     else:
...             return n[0] + recursive_sum(n[1:])
... 
>>> recursive_sum([1, 2, 3, 4, 5])
15
>>> sum([1, 2, 3, 4, 5]) # check against Python's built-in sum function

The “base case” in the function above prevents infinite recursion. A recursive function must, under some circumstance, return from the function without calling itself; otherwise, the recursion would continue forever.

(Sure, we could have also solved this problem by iterating over the list with a for loop and accumulating the sum in a variable. But the recursive_sum function is a helpful first step in learning to think about solving problems recursively.)

Exercise: The factorial of a number n (n!) is the product of all positive integers less than or equal to n. Write a recursive function that calculates the factorial of a number. (Don’t forget your base case!)

Traversing a nested data structure with recursion

The most common practical problem solved with recursion is traversing a nested data structure. The following program (print_dictionary_values.py) is an example of such a program. The program uses recursion to print out all of the values in a dictionary with nested dictionaries:

stuff = {
	'cat': {
		'name': 'Monsieur Whiskeurs',
		'fur': 'tortoise',
		'toy': {
			'name': 'plush catnip ravioli',
			'price': 'six dollars'
		}
	},
	'dog': {
		'name': 'Scrambles',
		'fur': 'golden',
		'outfit': {
			'scarf': 'tartan',
			'pants': {
				'color': 'green',
				'style': 'chinos'
			}
		}
	}
}

def print_dictionary_values(x):
	# if x is a dictionary, iterate through each value and call this function
	# on those values
	if type(x) == dict:
		for key in x.keys():
			print_dictionary_values(x[key])
	# otherwise, just print the value out
	else:
		print x

print_dictionary_values(stuff)

The program contains an arbitrary data structure (stuff) that has a number of nested dictionaries: dictionaries whose keys have values that are sometimes strings and sometimes other dictionaries (which themselves can have keys whose values are dictionaries). The print_dictionary_values function checks to see if its argument is a dictionary. If so, it iterates over every key in the dictionary and calls itself on the value. If not, it just prints out the argument.

Here’s where recursion comes into its own as a way of solving problems. Try to write a program that does this same thing with for loops—go ahead, try it! The advantage of recursion is it can elegantly cope with nested data structures of arbitrary depth.

Exercise 1: Make a similar program that prints out all elements from a data structure consisting of nested lists.

Exercise 2 (advanced): Make a similar program that prints out all elements from a data structure that consists of nested lists, dictionaries, and sets.

Exercise 3 (super advanced): Make a similar program that prints out the string attribute for every tag in a BeautifulSoup document.

Context-Free Grammars

From Markov to Chomsky: where n-gram analysis fails

What aspects of the syntax of human language does n-gram analysis not capture? Some are easy to catch, like these snippets from the output of a Markov chain algorithm (an order 4, character-level, source text The Waste Land):

And I ready, and gramophone.)

“What four army faces sings, slimy belly on the Metropole.

Anyone who has generated character-level texts with a Markov chain will recognize this problem: because an n-gram analysis only takes into account the immediate context of a word/character/token, there’s no way for it to recognize the fact that a quotation mark or parenthesis is occurring without its pair.

The same problem is demonstrated below, but in a slightly different way:

• That dog laughed.
• That dog over there laughed.
• That dog with the smelly ears laughed.
• That dog I told you about yesterday—the insolent one—laughed.

A human being can understand the structure of these sentences, and understand what the sentences mean. They’re all about laughing, and there’s a dog that’s doing the laughing.

But an n-gram analysis of these sentences won’t be able to tell us these (seemingly) simple facts: it can only tell us which words occur in which order. A partial word-level order 3 n-gram analysis of the sentences given above would yield the following:

that dog laughed
over there laughed
smelly ears laughed
insolent one laughed

If you tried to figure out the text’s meaning based purely on n-gram analysis, you’d come up with some pretty strange conclusions: the dog only shows up once, and the other n-grams seem to indicate that “over there,” “smelly ears” and some mysterious “insolent one” is doing the laughing the rest of the time.

Context-Free Grammars

From the examples above, we can see it takes more than just a knowledge of how words occur in sequence to understand (and generate) human language. More specifically, language has a hierarchical organization: sentences are composed of clauses, which themselves might be composed of clauses. A sentence, for example, is composed of a noun phrase and a verb phrase, and noun phrases and verb phrases can have their own internal structure, even containing other noun phrases or verb phrases. Linguists illustrate this kind of structure with tree diagrams:

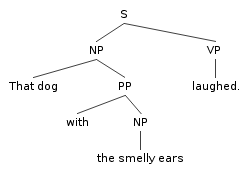
syntax tree

(generate your own tree diagrams with phpSyntaxTree)

Clearly, we need a model that captures the hierarchical and recursive nature of syntax. One such model is the context-free grammar.

A grammar is a set of rules. A context-free grammar defines rules in a particular way: as a series of productions. Our goal is to use these rules to generate sentences that have the structure of English. Here’s a mini-grammar of English that we can use for our initial experiments:

S -> NP VP
NP -> the N
VP -> V
VP -> V NP
N -> amoeba
N -> dichotomy
N -> seagull
V -> shook
V -> escaped
V -> changed

Key: NP = noun phrase; VP = verb phrase; S = sentence; N = noun; V = verb

Each rule specifies a “expansion”: it states that the symbol on the left side of the arrow, whenever it occurs in the process of producing a sentence, can be rewritten with the series of symbols on the right side of the arrow. Symbols to the left of the arrow are non-terminal; symbols to the right side of the arrow can be a mix of terminal and non-terminal. (“Terminal” here simply means that there is no rule that specifies how that symbol should be re-written.)

A symbol that appears on the left side more than once (like VP, N and V above) can be rewritten with the right side of any of the given rules. We’ll sometimes write such rules like this, for convenience, but it has the same meaning as the three N rules above:

N -> amoeba | dichotomy | seagull

Generating sentences

Okay! So let’s generate a simple sentence from our grammar. We have to choose a non-terminal symbol to start the process: this symbol is called the axiom, and it’s usually S (or whatever the “top level” rule is).

After we choose the axiom, the process for generating a symbol is simple. The process can be described like this:

• Replace each non-terminal symbol with an expansion of that symbol.
• If the expansion of a symbol itself contains non-terminal symbols, replace each of those symbols with their expansions.
• When there are no non-terminal symbols left, stop.

For this example, we’ll use S as our axiom, and stipulate that whenever we encounter a non-terminal symbol with more than one production rule, we’ll chose among those options randomly. Here’s what the generation might look like:

• S (apply rule: S -> NP VP)
• NP VP (apply rule: NP -> the N)
• the N VP (apply rule: N -> amoeba)
• the amoeba VP (apply rule: VP -> V)
• the amoeba V (apply rule: V -> escaped)
• the amoeba escaped

This isn’t a very sophisticated example, true, but the machinery is in place for producing very complex sentences. Of course, no one wants to do all this by hand, so let’s look at a program written in Python that automates the process of generating sentences from context-free grammars.

contextfree.py

The contextfree module defines one function, generate_list, which takes a grammar definition and then recursively generates strings from the grammar. It takes the axiom, and then “expands” that axiom out into a full sentence, following a set of steps very similar to the one we followed above. The above grammar, for example, will create output that looks like this:

The cat lusts after the weinermobile.

Here’s the code:

import random

def generate_list(grammar, axiom):
	"""Generate a list of tokens from grammar, starting with axiom. The grammar
		should take the form of a dictionary, mapping rules (strings) to lists
		of expansions for those rules. Expansions will be split on whitespace.
		Any token in the expansion that doesn't name a rule in the grammar will
		be included in the expansion as-is."""
	s = list()
	if axiom in grammar:
		expansion = random.choice(grammar[axiom])
		for token in expansion.split():
			s.extend(generate_list(grammar, token))
	else:
		s.append(axiom)
	return s

if __name__ == '__main__':
	import sys
	import json
	grammar = json.loads(sys.stdin.read())
	axiom = sys.argv[1]
	sentence = ' '.join(generate_list(grammar, axiom))
	sentence = sentence[0].upper() + sentence[1:] + "."
	print sentence

The code in the __main__ section reads in a grammar in JSON format, passed as standard input. You can run it with the included example grammar like so:

$ python contextfree.py S <test_grammar.json

But you can also just pass in a dictionary, as long as it follows the format below.

Grammars as dictionaries

It’s easy to write a grammar in the format of a Python data structure. Since a grammar is essentially a map (from rules to productions), it makes sense to use a dictionary to represent the data. The generate_list function expects a dictionary that looks like this (adapting from the example grammar above):

{
  "S": ["NP VP"],
  "NP": ["the N"],
  "VP": ["V", "V NP"],
  "N": ["amoeba", "dichotomy", "seagull"],
  "V": ["shook", "escaped", "changed"]
}

That is: rules are keys, and the values for those keys are all possible expansions (as a list of strings).

Recursive expansion

The generate_list function is where the work gets done: taking an axiom and turning it into a full sentence.

First, it creates an empty list (called s); this will contain the expansion for the given axiom. It then checks to see if the given axiom is a rule the grammar. If so, it chooses randomly from among the rule’s expansions. It then splits that expansion into individual tokens and calls generate_list on each of those tokens. Because generate_list returns a list, we use the extend method to add the result of expanding the token to the end of the list.

If the axiom is not a rule in the grammar, that means that it’s a terminal symbol—no expansion required—so we simply append it to the list. Finally, the function returns the generated list.

Here’s where it gets tricky

This is called recursion: when a function calls itself. Recursion is a handy tool in programming, especially for tasks that are self-similar—such as generating sentences from a context-free grammar.

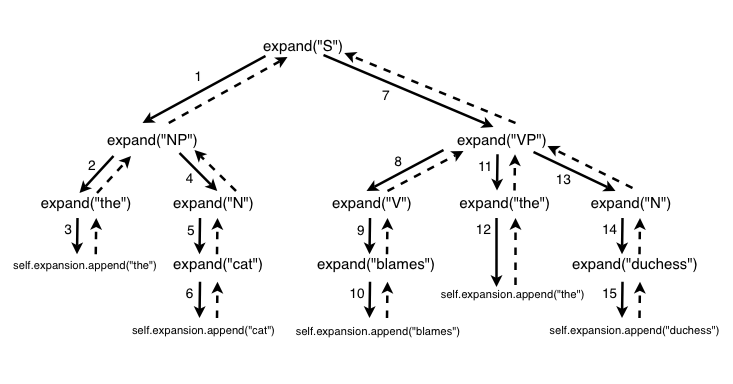
The idea here is that the expansion of one symbol—say, S—will set off a chain reaction of expansions of other symbols, until there are no more symbols to be expanded. A call to generate_list("S") will itself call generate_list("NP") and generate_list("VP"); a call to generate_list("NP") will itself call generate_list("the") and generate_list("N"); and so forth.

The diagram below illustrates the whole process (again, using our tiny sample grammar as an example). Solid arrows indicate a call to generate_list, dashed arrows indicate a return from generate_list, and the numbers indicate in which order the calls are performed.

(I need to update this graphic: just imagine it says “generate_list” wherever it says “expand”)

The order of calls is important. The generate_list method expands the left-most symbol to its full depth before it moves on to any more symbols.

Infinite recursion

The astute reader will notice that there’s the potential here for an infinite loop. Let’s say that the only expansion for the symbol NP looked like this:

NP -> NP or NP

Each attempt to expand NP would lead to another attempt to expand NP, which would lead to another attempt to expand NP, and so forth. The expansion would never complete, and Python would eventually complain that it had run out of memory.

One way to ensure that your context-free grammars will always completely expand is to check to make sure that every symbol has at least one expansion that will eventually lead to terminal symbols. For example, if we added the following rule to our grammar, we’d be okay:

NP -> the dog

(Of course, this grammar could potentially generate extraordinarily long strings, like the dog or the dog or the dog or the dog or the dog or the dog .... But it will eventually finish.)

Even more exercises

• Augment test_grammar.json to model some part of English syntax (or the syntax of some other language) that isn’t currently part of the grammar. Ideas: proper nouns, quotations, parenthetical remarks, adverbs, adverbial phrases, questions, etc. What’s easy to model, and what’s hard to model? Modify or extend the ContextFree class as necessary.
• Build a grammar that generates something other than English sentences. For example: stories, images, sound, computer programs, other grammars, etc. Modify or extend the ContextFree class as appropriate.

Further reading

• Generative gossip, a series of texts generated with this context-free grammar generator (including sample grammar)
• SCIgen, an automatic CS paper generator
• Universal Text Imitator (with interactive demo)
• Context Free is “a program that generates images from written instructions called a grammar. The program follows the instructions in a few seconds to create images that can contain millions of shapes.”